过程工业必须优化调节和先进控制,以确保在保证安全运行的同时,实现利润最大化。调节控制系统的稳定性是实现上述目标的关键因素。仔细地评估工厂并进行控制回路的整定,一般可以提高系统的稳定性。
大多数控制回路由比例、积分、微分(PID)控制器来控制。工厂人员深入了解如何整定这些回路,就可以提高运行质量和效率,同时确保工厂的安全。此外,实现调节控制系统的稳定性,是构成先进过程控制应用的基础,而且能够进一步优化运行。
除了维持安全运行外,通过降低排放和能源消耗,提高设备的使用寿命,稳定的调节控制系统可以为工厂增加收益。利用自动诊断控制回路,可以降低手动运行的要求,节省人工时,提高产品的一致性。
控制回路基础
在典型的控制回路中,必然会有一个受控参数,比如温度或者压力。该参数被称之为过程参数(PV)。一般由传感器测量过程参数,被测量的变量作为反馈回传给闭环控制系统的控制器。
对过程变量的期望值,比如在温度控制系统中的40℃,被称之为设定参数(SV)。举个例子,如果过程参数只有30℃,那么控制器就会动作,调整其输出值以增加温度。
限值就是过程能够安全、高效运行的界限。比如,在某些工艺过程中,温度达到42℃时,液体中的某种化合物就会被破坏。因此在整个过程中,温度必须保持在该限值之下。但是,如果过程运行在36℃以下,则比限值低的太多,就不能保证质量,生产过程的效率也随之降低。因此,控制过程变量(PV)的目标就是在最小的波动下,尽可能的将其与设定值靠近。当波动最小化时,设定值就可更加靠近限值,从而改善运行。
PID控制器
PID控制器是过程工厂中最常用的控制器类型,在典型工厂中,超过95%以上的控制回路使用PID进行控制。在提高质量、能源利用效率和产能方面,常用的PID控制器是一个非常有效的工具。
在大多数运行环境中,PID控制器都具有优良的性能,可以以一种简单、直接的方式对其操控。PID可以是单体的,也可以是嵌入式的;可用于一个或多个控制回路。它们可以与顺控逻辑和先进控制功能结合使用,组成复杂的自动化系统。
PID运算包括三个基本部分:比例、积分和微分。任何一个基本元素的设置都可改变,以期实现最优的响应特性:在最小波动的情况下,尽可能将过程值维持在设定值附近。每个基本元素都与某个任务相关,对控制回路有特殊的影响。
PID控制器接收来自传感器的过程数据,确定过程测量值和期望设置值之间的偏差(误差)。然后基于偏差,计算出期望的控制器输出量或者操作量(MV)。操作量作用于最终控制元件(例如,蒸汽阀门),从而影响过程,改变过程参数(见图1)。
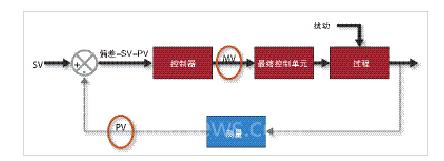
用于计算PID控制器整定参数的技术有很多种。大多数都是基于某个数学模型,该模型专门为最终控制对象、过程和测量的组合体开发。
描述控制器的模型就是PID的算法。如果能为过程(最终的控制元件,过程和测量)确定模型,那么就建立了整个控制回路的数学模型。在这一点上,控制器的整定就变成了控制器整定参数(比例、积分和微分)和过程模型参数的匹配,优化上述三个PID常数,来实现期望的响应特性。
在现实世界中,影响系统的并不仅仅只是控制器输出信号。在环境中,经常会有一些因素会导致偏移,比如环境噪音。一般称之为扰动。尽管在控制过程工艺时,必须考虑扰动因素,但实际上,会有意识的引入临时扰动以启动控制器的整定。
PID控制器的整定
PID控制器的整定过程包括如下五个步骤:
1. 引入扰动至控制回路;
2. 匹配所得结果与数学模型;
3.利用整定关系,计算控制器参数;
4. 应用新的比例、积分和微分参数;
5.文档记录结果。
PID控制器整定的第一步包括:在回路中引入扰动,产生新的控制器输出(CO)。这称之为阶跃测试。引入控制回路的扰动必须足够大,过程参数能够产生明显的响应,而且必须能够将其从系统噪音中区分出来。不可测量的扰动能够损坏过程数据,所以能产生更大输出的阶跃会更好些(见图2)。
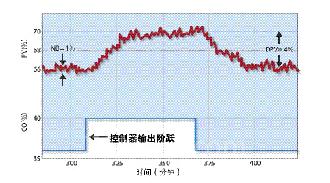
图2 阶跃测试应显示输入和控制器输出变化之间的动态关系。上图显示CO阶跃变化导致PV值显著变化。
自稳定过程vs.非自稳定过程
描述过程,使用多少模型类型都可以。但是在选择模型前,必须首先确定过程是自稳定类型还是非自稳定。由于不同的过程需要不同的数学模型,所以这个测定对控制器的整定十分关键,。
因为过程有其内在方法,通过过程参数整定来平衡控制器输出量的变化,所以在控制器输出引入变化后,只要输出量和扰动量保持稳定,自稳定过程最终会找到一个稳定状态。例如,在流量控制回路,如果一个阀门开度增加10%,流量会增加到一个新的数值并稳定下来,直到阀门再一次移动。大多数的过程是自稳定类型的。
但是,在非自稳定过程中,过程参数持续变化,直到输出量恢复到初始位置。对非自稳定过程,过程参数持续按照与控制器输出变化量的关系,线性增加或降低。这就意味着非自稳定过程很难控制。非自稳定过程的一个例子就是改变水箱的液位。如果更多的流体流入水箱,液位就持续增加;如果更多的流体流出,液位则持续降低。
自稳定过程的控制回路整定要比非自稳定过程要简单一些。如果非自稳定过程回路的整定不正确,很容易而且很快就会发生负面结果。在非自稳过程中,引入输出量的变化后,它很难达到新的平衡状态,这很容易导致问题。比如,液体溢出或者流干,这可能会导致设备(泵)的损坏、环境的破坏、或者重大的安全事件。
自稳定过程需要比例和积分(偶尔需要微分)控制模式,以实现良好的控制性能。尽管命名上比较类似,但是非自稳定过程对积分模式的依赖要少的多。不同的过程模型需要不同的整定规则。
使用建模
阶跃测试完成后,相关的过程类型就确定了,下一步就是模型和数据的匹配。建模是理解过程数据最好的途径之一。一般情况下,一阶加纯滞后(FOPDT)动态模型就足以描述过程响应,计算出最佳的整定参数。
在这个模型中,过程参数是被测的过程变量,输出信号是被控变量。FOPDT模型很简单(低阶、线性),只是近似的描述了真实过程,可以由下面的公式描述:
集总参数过程模型
集总参数模型是一个FOPDT模型。该模型利用简单的线性公式描述过程响应,该公式包含三个参数:增益(Kp),时间常数(tp ),和死区时间 (0p )。对于集总参数模型,根据过程控制回路的特性:自稳定过程(流量,温度等)和非自稳定过程(液位),需要两种不同类型的模型。
因为非自稳定过程更难控制,必须使用不同的模型来描述这个过程,可以用以下公式来描述:
调节相互关系
有很多种调节相互关系的方法,可用于计算PID参数整定。
Ziegler-Nichols 和 Cohen-Coon是最流行的两种计算参数整定的方法。这两种技术强调响应的速度。内部模型控制(IMC),也被称为“Lambda法则”,提供了一种替代方法,该方法可以平衡响应速度和控制器稳定性,或称之为鲁棒性之间的关系。IMC调节可用于线性和非线性过程,它的FOPDT响应要比其它技术的响应要平滑的多。
IMC调节基于这样一个概念:使用精确的过程模型,可以实现理想的控制。但是,由于外部干扰会影响过程,导致模型和实际过程之间的不匹配,会产生错误的结果。结果就是,在其它模型多有错误发生的高频领域,IMC的设计中有用于补偿扰动和模型误差的方法,包括滤波和补偿器。
和其它整定过程一样,必须对IMC进行阶跃测试来确定其过程特性。确定完集总参数过程模型后,必须为控制回路选择期望的闭环回路时间常数(tCLtaucl )。
如果闭环回路时间常数太大,控制回路就比较慢。因此,较小的值(tCL)对应较快的控制回路。但是如果设定的闭环控制回路时间常数(tCL)比FOPDT过程的时间常数(tp)小,那么IMC就会丧失其调节优势。
一般情况下,tCL值应设定为tp 值的1到3倍。很多情况下,将tCL设定为 3 倍的 tp是实现稳定控制回路的最佳选择。因此,在确定FOPDT过程模型后,IMC技术只有一个可整定参数:闭环时间常数。通过改变闭环时间常数,控制器速度可以变得更快或更慢。
由于控制器的积分时间被设置为和过程时间常数相等,IMC有一个缺陷。 如果过程时间常数较长,则意味着控制器的积分时间也比较长—长的积分时间会导致从扰动中恢复的时间比较长。
正确整定PID控制器,不是一个简单的过程,但是它是提高过程产量、质量和安全性的最好的方法之一。通过改进PID整定,实现稳定的调节控制系统,可以安全的将设定值设定在限值附近,同时降低过程值的波动,从而减少过程的低效率。
然而,采集数据和执行所有的数学模型,可能非常困难而且是耗时的。幸运的是,先进的软件能够简化PID整定,降低可能发生的错误。
不管PID回路的整定是手动,还是借助于回路整定软件,每个控制回路性能提升都会带来整个过程工厂整体性能的巨大改进。
(转载)





