作为转向系统的转向梯形机构,文献运用参数方程对转向梯形机构进行了建模和分析、研究,但对转向传动机构分析和计算的几何法就十分不便,特别是结构复杂的独立悬架的传动机构计算更为不便。大型专用汽车的转向轴多在二轴以上,有的甚至多达五轴,其转向性能的好坏直接影响车辆行驶的灵活性、操纵稳定性、经济性和轮胎的使用寿命,而且车轴越多,转向对车辆行驶影响越大。本文运用参数方程法,对转向传动机构的各点用坐标参数来表示,建立参数方程求解、分析,提出了一种可运用于多轴转向的传动机构优化设计的计算方法,达到各轴转向协调的目的,提高车辆行驶的灵活性、操纵稳定性和经济性。
2 转向时各转向桥的理想转角关系
图1为某前双桥转向底盘转向时各转向轴内外转向轮的理想转角关系,由于不研究转向梯形机构,只讨论转向传递关系,所以只分析内侧的车轮的转角关系。
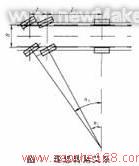

3 一桥传动机构传动模型
多轴转向汽车一般通过连杆机构来保证同一侧车轮在转向时绕同一瞬心作圆周运动。下面以常用的连杆机构中第一轴摇臂的摆角与车轮转向臂转角的对应为例,说明连杆机构的运动关系(如图2)。
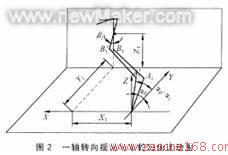
图2中:A1为车轮转向节臂初始位置;Al′为车轮转动角a1转向节臂位置;B1为一桥传动摇臂初始位置;B1′为车轮转动a1′角一桥传动摇臂位置。


4 一桥梯形机构传动模型
根据文献的梯形机构的建模方式,将梯形机构简化为平面机构,则一桥梯形机构得一桥外轮转角a1′与 一桥内轮转角a1之间关系(如图3)。
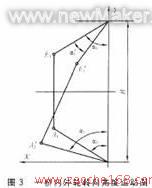
图3中:A1为内轮转向节臂初始位置;A1′为内轮转动a1角转向节臂位置;El为外轮转向节臂初始位置;E1′为外轮转动a1′角一桥传动摇臂位置。


一桥至二桥之间的传动模型
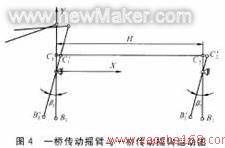



7 设计优化
由(4)、(6)、(8)、(9)、(10)式可计算出一桥车轮内、外轮的每一转角与二桥车轮内、外轮的每一转角的对应数据,将该数据与由(2)式计算出的理论转角数据进行比较。考虑到轮胎侧偏角,理论与实际转角差可由轮胎产生侧偏角来弥补。对应于一桥内轮的每一转角,一、二桥外轮实际转角与理论转角最大相差在2°范围内且在小转角范围内(内轮转角≤20°)。右轮实际转角与理论转角相差更小时,可认为设计合理。若超出该范围就需对各杆件的参数进行调整,以满足要求,得到理想的协调关系。
8 结论
本文针对两轴转向车辆的转向传动机构进行了优化设计,同时对多轴转向的转向机构优化设计具有较普遍的指导意义,其原理一样,方法相同,而且不用建立统一的坐标系,每个转向轴分开计算、分析,方法简单易懂,操作性强,特别是适用于用计算机进行计算,使优化设计方便快捷,具有较强的理论意义和参考价值。
相关阅读:
•
•
•
•
•
•
•
•
•
•
(转载)





