自上世纪80年代以来在我国的一些工程车辆上开始引进该项技术,随后我国的一些研究人员对此项技术开始了研究,并取得了一些成果油气悬架技术始于上世纪60年代特·卡尔朋发明的油气悬挂,与传统的悬架(钢板弹簧式)相比具有单位储能比大、刚度阻尼的非线性、结构紧凑、控制方便等优点,在国外的工程车辆及特种车辆上获得了广泛应用。。但仍有以下问题:[1] [2] [3]
(1)设计油气悬架时,迄今尚未有简单易行的计算公式以供工程设计人员在设计和校核时选择和使用。
(2)目前已经开展的研究工作大都停留在理论上,仿真较多,试验较少。
(3)目前国内进行的研究工作都是针对某一车型(引进)的油气悬架所展开的,缺少对油气悬架的基础性、系统性研究。
鉴于以上问题,对油气悬架技术进行理论分析和试验研究是适时和有必要的,本文以最基本的单气室油气分离式油气悬架为研究对象,对其进行理论建模及试验研究,以期揭示油气悬架的基本特性。
1 单气室油气悬架的工作原理
图1为单气室油气分离式油气悬架的结构原理图。整个悬架缸内部形成3个腔,即悬架缸无杆腔(Ⅰ腔);悬架缸有杆腔(Ⅱ腔);活塞杆的内壁形成的空腔——中心腔。活塞杆及活塞组件2上设有单向阀3和阻尼孔4使中心腔与Ⅱ腔相连通。当悬架处在压缩行程(活塞杆向上运动)时,Ⅰ腔和中心腔的油液受到压缩向两个方向运动,一部分油液经过单向阀3和阻尼孔4流入Ⅱ腔;另一部分油液进入蓄能器,使气室容积减小,氮气压力升高。在这一过程中由于单向阀3和阻尼孔4同时使中心腔与Ⅱ腔连通,油液流经单向阀3和阻尼孔4的流速较低,产生的油液阻尼力比较小,因此主要由蓄能器内的气体受到压缩产生弹性作用来抑制活塞杆的向上运动,相当于传统悬架系统的弹性原件——弹簧。
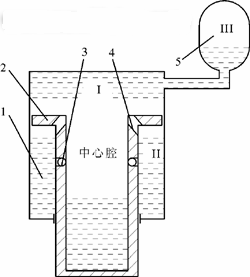
当悬架处于伸张行程(活塞杆向下运动)时,单向阀3处于关闭状态,Ⅱ腔的油液受到压缩,迫使Ⅱ腔的油液通过阻尼孔4向中心腔流动。油液只经过阻尼孔流动,流速较高,产生较大的阻尼力,抑制了活塞杆的向下运动,从而迅速地衰减振动,相当于传统悬架系统的阻尼元件——减振器。
2 单气室油气悬架的数学模型的建立
建立数学模型时遵循以下假设:
(1)流体流动为定常流动
(2)忽略温度变化对系统的影响
(3)忽略运动时的库仑摩擦力和粘性摩擦力
图2为单气室油气分离式油气悬架物理模型。
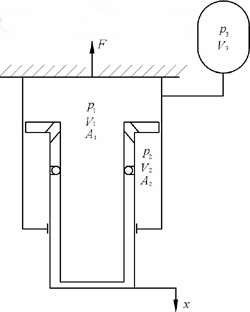
图中符号:
p1、A1为无杆腔压力、截面积
V1为无杆腔和中心腔油液的总容积
p2、A2、V2为有杆腔压力、截面积和总容积
p3、V3为蓄能器内气体压力、容积
F 为悬架缸缸筒输出力,拉力为正,压力为负
x为悬架缸活塞杆的位移,向下为正
假设悬架缸筒固定不动,活塞杆及活塞组件相对缸筒运动。
输出力方程:
F=p2A2-p1A1 (1)
流经阻尼孔和单向阀的总流量:
Q=A2- (2)
dV2=(3)
式中:dV2——Ⅱ腔内液体因油液压缩性而引起 的在时间dt内的体积变化量
K——油液的体积弹性模量
流经阻尼孔的流量:
Q1=CdA01sign()(4)
式中:Cd——流量系数
A01—— 阻尼孔的过流面积
sign()=(5)
ρ——油液密度
流经单向阀的流量:
Q2=CdA02sign() (6)
式中:A02——单向阀的过流面积
对于蓄能器内气体有
p3V3r=p30V30r (7)
式中: p30,V30蓄能器内气体初始压力和体积
r——气体多变指数。对理想气体,在等 温过程时r=1,绝热过程时r=1.4。而实际气体的多变指数在绝热过程中可取到1.7[4]
V3=V30+(A1-A2)x+ΔV1+ΔV2(8)
式中:ΔV1,ΔV2分别为大小腔内液体由于油液压缩引起的体积变化量且有:
ΔV1=(9)
ΔV2= (10)
而对于大小腔液体有:
V1=V10+A2x-ΔV1-ΔV2(11)
V2=V20-A2x (12)
式中:V10 、 V20分别为大小腔液体初始体积
对于蓄能器出口有:
p3-p1=ξpsign(13)
式中:ξ——压力损失系数
A3——蓄能器出口处油管断面积
Q3——流经蓄能器管口的流量
Q3=(A1-A2)(14)
式(1)~(14)即为单气室油气分离式油气悬架的非线性数学模型,想求出上述非线性方程组的解析解是不可能的,只有运用仿真解法求其数值解。
3 单气室油气悬架的试验研究
为验证以上数学模型的正确性,需对油气悬架进行台架试验。悬架的试验台架原理可参考文献4。
本文的试验设备是徐州工程机械集团有限公司技术中心结构振动疲劳试验室的整车道路模拟试验台。整套设备和仪器是德国卡尔申克公司生产的多轴激励电液伺服试验系统。该套设备可实时产生正弦波、随机波等各种幅值和频率的信号,作为驱动信号。试验台采用S59 数字控制设备和VAX工作站进行控制和记录, 是专门进行油气悬架试验研究的高精尖设备[5]。
试验中采用标准正弦信号作为激励信号,具体参数见表1,通过工作站记录输出信号。
4 试验与仿真结果的比较
以液压缸参数作为输入参数,应用MATLAB软件进行仿真。模型中参数选取见表2。
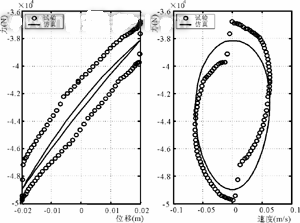
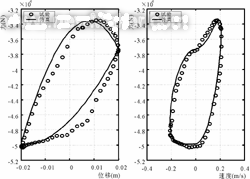
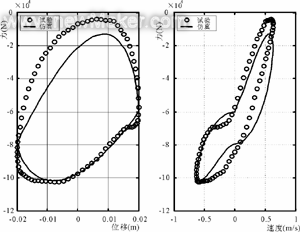
由于篇幅所限本文仅给出频率f=0.5,1.67,5 Hz,幅值A=20 mm时的试验数据与仿真结果的对比图(见图3,4,5)。
5 结论
(1)油气弹簧悬架试验数据与仿真结果基本吻合,说明所建立的油气弹簧悬架的非线性数学模型是基本正确的,可以用该模型进行油气悬架的特性仿真。
(2)在低频激励时,试验数据在速度为零处有明显的的突变,突变值约为3 000 N,与仿真结果相比有明显的误差。经分析,主要原因为数学模型中没有考虑液压缸的静摩擦力。据文献6的研究,此种典型减振器的静态摩擦力为500~5 000 N,由于本试验所用液压缸为新液压缸,故静态摩擦力值应较大,这从图3中可以较清楚地看出。而在高频激励时,液压缸处于震颤状态,静态摩擦力很小,此时液压缸输出力很大,相对误差较小,因而在图上看不出明显的突变。
(3)在高频激励时仿真的特性曲线与试验数据在走势上有一定的误差,经分析,其原因为所建立的数学模型中没有考虑液压系统的温升。但从比较图中可以看出,误差较小,对于一般的理论分析与工程应用,所建立的数学模型已经能满足精度要求。
相关信息:
•
•
•
•
•
•
•
•
•
•
(转载)





