汽车车架是车辆支承连结各种零部件的基体,在使用条件下,车架的主要受力件纵梁在自重及载荷的作用下会发生变形呈下挠趋势,对轴距较长的车架或承受载荷较大时纵梁下挠弯曲变形尤为明显; 因此,具有足够的强度和弯曲刚度是对车架纵梁的基本要求。为提高车架纵梁的强度和弯曲刚度,通常的解决办法是增加纵梁截面的抗弯模量或采用更好的材料; 即提高所用材料的强度、增大纵梁截面的面积或尺寸,但这无疑会增加车辆的成本、重量或占用较多空间,因而这些方法有其局限性。
本人在桥梁建筑行业干过几年,故想就如何提高梁的承载力、减少梁的下挠变形与从事车架设计的人员交流交流。
其实,使用状态下的车架纵梁与大多数桥梁一样可近似为简支梁,工况也类似(交变载荷),为提高桥梁的刚度和承载力,从前的桥梁设计也是采用增加梁截面的抗弯模量或改换材料的办法,自从将预应力技术应用于桥梁结构设计后,桥梁结构明显轻量化;
往简单说,预应力技术就是利用预应力筋来承受梁中最易发生破坏的受拉部位的负荷,尽可能的利用梁中各部分构成材料的性能,对预应力技术有兴趣的朋友可去查阅相关书籍。
本文只准备通过对一组具体的槽型梁在施加预应力前后在不同荷载下的挠度进行对比来说明槽型梁施加预应力前后的效果。
在载重车车架中,槽型断面的纵梁是应用最为广泛的结构形式。设有如图1所示的简支梁A,受均布载荷q作用在梁上,梁的长度L=5000mm,其材料弹性模量E=2.1×105 Mpa,梁A截面尺寸如图2所示
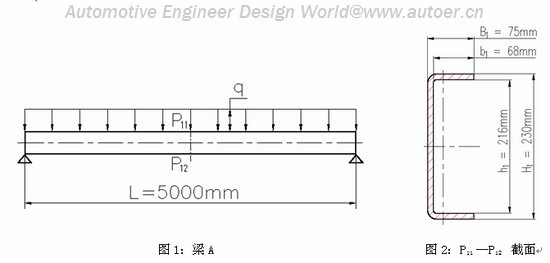
图1:梁A 图2:P11 —P12 截面
梁A截面积 S1 =B1× H1-b1× h1=2562mm2
梁A惯性矩 Jx1 =(B1× H13-b1× h13)/12=18936806(mm4)
梁A抗弯截面模数 Wx1 =(B1× H13- b1× h13)/6H1=164668(mm3)
梁A在承受均布载荷q后
梁A最大弯矩 Mmax1 =q× L2 /8
梁A上侧P11 点最大压应力 σP11max =-Mmax1 / Wx1
梁A下侧P12点最大拉应力 σP12max = Mmax1 / Wx1
梁A最大挠度 fmax1 = 5q× L4 /(384E×Jx1 )
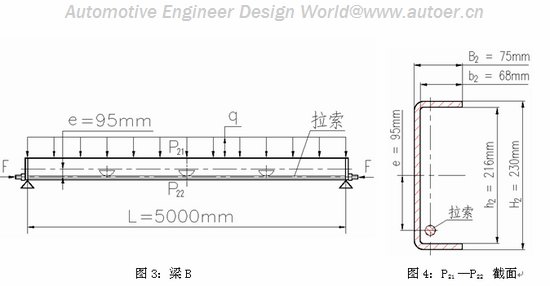
图3:梁B 图4:P21 —P22 截面
在图3所示的梁B中,梁下部通过张紧的拉索施以预紧力F=5.5×104N,预紧力F偏心e=95mm(预紧力F作用位置可进一步优化),梁B的长度L=5000mm,材料弹性模量E=2.1×105 Mpa,梁B截面尺寸如图4所示,则
梁B截面积:S2 = S1 =2562mm2
梁B惯性矩:Jx2 = Jx1 =18936806(mm4)
梁B抗弯截面模数:Wx2 = Wx1 =164668(mm3)
梁B未承受均布载荷q时,仅施加有偏心预紧力F的梁B可视为受弯矩 M2=F•e的压杆,梁B因F及M2所产生的负荷为:
弯 矩: M2 =F•e=5.225×106N•mm
梁B上侧P21点的预拉应力:σP21 = M2/ Wx2-F/S2=10.3 Mpa
梁B下侧P22点的预压应力:σP22 = -M2 / Wx2 -F/S2= -53.2 Mpa
挠 度:f2=-M2×L2/(8E×Jx2 )= -4.1mm
梁B在M2作用下略呈反拱状,从上式可看出,调整M2可改变f2的大小;梁B承受均布载荷q后,梁中产生的负荷为:
弯 矩: M max2 = q× L2 /8
梁B上侧P21点最大应力:σP21max = -M max2 / Wx2+σP21
梁B下侧P22 点最大应力:σP22max = M max2 / Wx2+σP22
挠 度:fmax2 = 5q× L4 /(384E×Jx2 )+ f2
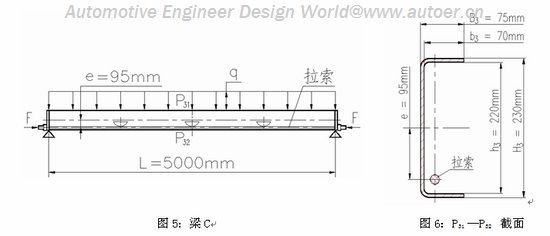
图5:梁C
图6:P31 —P32 截面
图5所示的梁C与梁B受荷载情况相同,但梁C截面尺寸如图6所示
梁C截面积:S3 =B3× H3-b3× h3=1850mm2
梁C惯性矩:Jx3=(B3× H33-b3× h33)/12=13930417(mm4)
梁C抗弯截面模数:Wx3 =(B3× H33- b3× h33)/6H3=121134(mm3)
梁C未承受均布载荷q时,仅施加有偏心预紧力F(预紧力F作用位置可进一步优化)的梁C亦可视为受弯矩 M3=F•e的压杆,梁C因F及M3所产生的负荷为:
弯 矩: M3 =F•e=5.225×106N•mm
梁C梁上侧P31点的预拉应力:σP31 = M3/ Wx3 - F/S3=13.4 Mpa
梁C梁下侧P32点的预压应力:σP32 = -M3 / Wx3 - F/S3= -72.9 Mpa
挠 度:f3=-M3×L2/(8E×Jx3 )= -5.6mm
梁C承受均布载荷q后,梁中产生的负荷为:
弯 矩:M max3 = q× L2 /8
梁C上侧P31点最大应力:σP31max = -M max3 / Wx3+σP31
梁C下侧P32 点最大应力:σP32max = M max3 / Wx3+σP32
挠 度: fmax3 = 5q× L4 /(384E×Jx3 )+ f3
分别取不同的均布载荷q值代入上述各式,算得结果如下表:
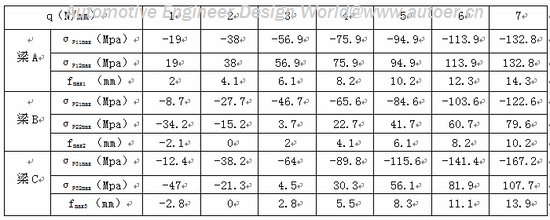
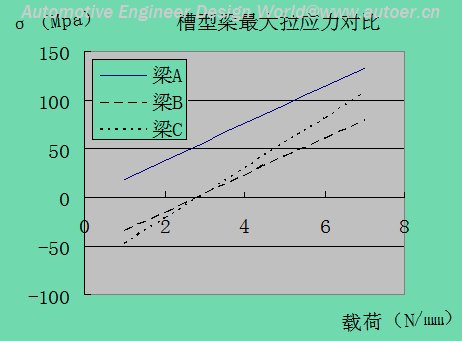
从上表中的计算结果可看出:梁B与梁A虽然具有相同的横截面积,但梁B承载后下挠变形比梁A小,且梁B内的应力幅也较小;而梁C尽管与梁A承受同等的载荷,但横截面积比梁A减少了27.8%,且梁C承载后的下挠变形依然小于梁A。
这是由于在拉索张力作用下使梁B和梁C内产生的预应力抵消了部分因受载而产生的应力,从而减小了梁的变形,以及梁B和梁C在预应力作用下产生的反拱补偿了部分承载后的下挠变形的缘故。
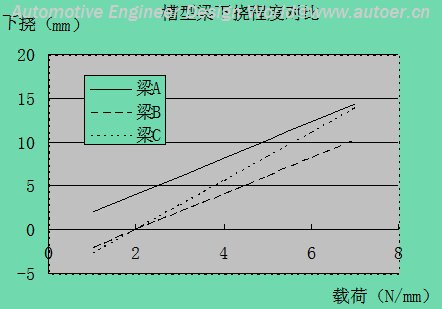
通过上述槽型梁在施加预应力前后在不同荷载下的对比说明:对槽型梁施加适当的预应力可获得以下几个效果:
1.可有效减小槽型梁的下挠变形,有利于提高槽型梁的刚度和承载能力;
2.可有效降低槽型梁内的应力幅,有利于提高槽型梁的抗疲劳性能;
3.对于承受同等的载荷,槽型梁可以采用更小的构件截面从而可减轻结构自重,有利于节能降耗。
当今,预应力技术已广泛应用于大型建筑结构且卓有成效,建议汽车设计师考虑将这一技术结合到车架设计中,以拓展车架结构轻量化的新途径。





