| [摘要> 本文对给水泵站调速改造方案确定进行了研究。根据系统工程最优化的观点,用动态经济的方法建立了以泵站年耗电费与调速设备年费用之和为目标函数的水泵选型数学模型,通过求出调速前的泵站年费用和不同的调速方案的年费用,然后进行比较,确定调速改造方案可行性和最佳调速改造方案。在模型的求解过程中,还建立了以泵站运行功率最小为目标函数的优化运行数学模型,考虑了流量、转速、扬程等各项约束条件,着重分析了有、无调速泵两种情况的流量、轴功率、装置总效率的求法,最后借助计算机实现了整个模型的求解算法。
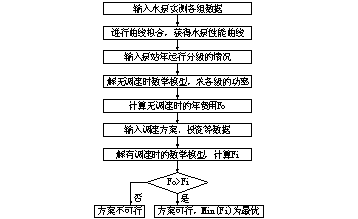
[关键词> 给水泵站 调速 年费用 最优化 一、引言 给水泵站调速供水因其具有良好的节能效果而越来越得到广泛应用,一些无调速泵的泵站也已经或准备进行调速改造。但是,有些泵站在调速改造后,其节能效果不明显,调速设备投资成本回收年限较长,并没有达到预期的效果。究其原因,除运行方面外,主要是调速改造方案不合理。因此泵站在调速改造时一定要对方案的可行性及最佳调速泵台数进行研究。国内有一些文章比较提倡“两台泵调速”的观点,但只作了定性的讨论[1>。本文试图用计算机从量的角度对调速改造方案可行性和调速泵台数确定进行研究。 二、给水泵站调速改造的目的及方案评价方法 1、给水泵站调速改造的目的 调速改造的主要目的是使泵站运行工况与供水对象所需工况一致,从而最大限度地减少剩余水头,节约电能。另外,除节能外,同时调速供水还能满足区域水量水压要求,保持管网压力稳定,减少爆管事故,降低漏水率等。 2、给水泵站调速改造方案评价方法 评价给水泵站调速改造方案必须从技术经济的角度出发,求得改造前的泵站年费用F0及拟采用的各种调速改造方案的年费用Fi,如果Fi< F0 ,则泵站可以进行调速改造, Fi中最小的方案即为最佳调速改造方案,否则该泵站调速改造方案不可行。 三、给水泵站调速改造前后年费用的确定 (一)、水泵性能曲线方程 实践表明,在额定转速下,泵的Q-H、Q-N曲线可以用多项式表示[2>。一般泵站在运行一段时间后,水泵特性曲线与原样本曲线有些偏差,可以通过实测若干个水泵工况点,通过最小二乘法进行曲线拟合,获得水泵性能曲线方程,研究表明取m=4具有足够的精度: (二)、改造前后的年费用 设泵站的运行工况可分为Nduty级,由动态经济分析方法,其年费用可用下式求得[3>: 式中 F——泵站年费用,元 显然,对于一个具体泵站的技改项目,除Ni外,其余的变量值皆易求得。下面重点介绍Ni的求法。 (三)、总功率Ni的计算 1、数学模型的建立 要求得Ni必须确定泵站在第i级供水的最优运行方案,对于同一级供水工况(Qi,Hi),不同的开机方案泵站的总能耗不同,能耗最小的开机方案即是泵站在该分级下的最优运行方案。可建立如下数学模型: (1)目标函数: 其中Num——泵站内水泵台数 ηi, j——水泵机组的总效率 ωi, j——状态函数,ωi, j =0 表示第j台水泵停运,ωi, j =1 表示第j台水泵运行 Ni, j——第i种型号第j台水泵的轴功率 (2)约束条件: 1)水泵特性曲线方程: 式中Hi, j––—第i种型号第j台水泵的扬程 Qi, j——第i种型号第j台水泵的工作流量 2)流量约束: 式中Qi——泵站第i级供水流量 3)单泵流量约束:水泵流量过小或过大都会导致其效率低,故要求水泵运行时流量界于最大最小流量之间,对定速泵有: Qj,min ≤ Qi,j ≤ Qj,max 其中Qj,min、Qj,max——第j台泵的最小最大流量,根据水泵的特性曲线选定; 对变速泵有: 式中nj ——第j台水泵的额定转速 nj′——第j台水泵调速运行转速 4)转速限制: 可根据调速设备的性能和水泵机组的特性确定调速范围nj,min ≤ nj ≤ nj,max 5)扬程限制: 对于定速泵有Hi,j ≥ Hi 对于调速泵有Hi,j = Hi,这里Hi为泵站第i级供水扬程 2、数学模型的求解 上述数学模型是一个混合型非线性规划问题。其求解步骤为:由机组要求和水泵并联运行的内在规律首先求出每台泵的流量Qi, j,对于定速泵,可用Ni, j= i(Qi, j)直接计算单泵的轴功率;对于调速泵,可据水泵相似原理由转速nj求得Ni, j 。而后选择状态函数ωi, j进行组合,通过比较各组合的功率,得出最优组合,即功率最低的组合。 (1)流量Qi, j的确定 整个模型的求解中,Qi, j的确定是至关重要的。不同的水泵规格、是否有调速装置,其Qi, j值是不同的。严格地说,同型号水泵由于水泵吸压水管道及其出口阀的开启度的不同而导致Qi, j不同,但文中为了简化计算,设定同型号定速泵的Qi, j值相等,同型号调速泵转速相等且泵站中水泵型号最多为两种,并只考虑容量大的水泵调速。下面将Qi, j的确定分成水泵是否有调速装置两种情况。 1)当水泵无调速装置时: 对于同型号水泵,各水泵的工况是相同的,设在并联工作曲线上的工况点为A,则有: Qi,j = QA / Num 对于不同型号水泵,情况稍有不同。设有Ⅰ型水泵(Num)1台,m台运行,工作流量为Q1, j ,Ⅱ型水泵(Num )2台,n台运行,工作流量为Q2, j ,根据水泵并联工作原理,有: 0 这是一个非线性方程组,借助计算机可以快速求解。、 2)调速泵:显然,只有泵站的工作情况与供水对象的需求一致时才是最理想的情况,设有Ⅰ型水泵(Num)1台,其中l台调速运行,m台定速运行,Ⅱ型水泵(Num)2台,全部采用定速泵,其中n 台运行,则由f1(Q1, j)= f2(Q2, j)= HA ,可得到定速泵的流量Q1, j 、Q2, j;按照流量约束条件,得调速泵的单泵流量为Qspd=【QA-(m-l)Q 1,j- nQ2,j】/l 。 (2)各泵的轴功率Ni, j的确定 获得单泵流量Qi, j后,根据水泵Q-N特性曲线方程和调速工况相似原理,可得到各泵的轴功率Ni, j 。 (3)单泵装置总效率ηi, j的确定 对于一台水泵机组,ηi,j为传动效率、电机效率、调速设备调节效率三部分之积。 确定数学模型中所有的变量后,不断地变换状态函数ωi, j进行水泵组合,求出各水泵组合的耗电功率,得出目标函数的最小值。 四、算法实现方法 上述算法可以编制计算机程序,其具体做法是求出调速前的泵站年费用F0,不同的调速方案的年费用Fi ,然后进行比较,确定方案可行性或最佳改造方案,其主要算法程序流程如图1所示。 五、结束语 给水泵站在进行调速改造时,一定要获得真实的水泵特征参数,再从量的角度进行技术经济比较,确定最佳改造方案。如果盲目认为调速改造一定节能,对泵站都进行改造,则可能达不到预期的效果。值得注意的是,在确定改造前后年费用时,要获得设备投资、折现率等有关参数,其中选用不同的调速设备,价格相差很大,可能会得出不同的结果;在确定数学模型的有关限制条件时,如转速上下限,要结合机组的实际情况。 参考文献 [1> 李名锐. 水泵调速机组效率变化与选泵. 哈尔滨建筑大学学报, 1995.6, 58-63 [2> 姜乃昌. 水泵及水泵站(第四版). 北京:中国建筑工业出版社, 1998.6 [3> 沈德康. 技术经济(第一版). 北京:中国建筑工业出版社, 1991.9 |
(转载)